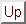
The HSRL is a dual channel vertically pointing lidar with high spectral resolution. This instrument makes point measurements (line measurements in time) of the atmospheric structure advected over its position by the wind. The HSRL transmits radiation at a wavelength of 532 nm and was used to determine the visible aerosol backscatter cross sections per unit volume, optical depths, and if the particulate and gaseous absorption are negligible, aerosol backscatter phase functions. The HSRL has an advantage over single channel lidar systems because it separates the backscattered radiation into a part due to aerosols and a part due to molecules. This separation is possible because the signal backscattered from the molecules is Doppler broadened while the larger, bulkier aerosols have little effect on the wavelength of the scattered light. This two channel approach enables a direct calculation of the atmospheric extinction and aerosol backscatter cross sections per unit volume. The advantage of this system over a single channel lidar system can be seen by first examining the single channel lidar equation and then the dual channel lidar equation. The equation for a single channel lidar system is:
where:
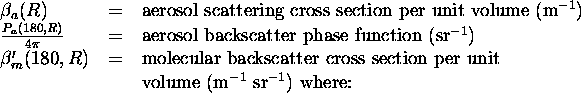
Equation 1 contains two unknowns, 
and
(since 
can be calculated from a
radiosonde profile). This equation can
be solved by either finding a
relationship between 
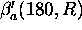and 
or by using
a calibration source to directly determine one of these two variables. In
the former case, the Klett method has been used to solve the lidar equation.
This method assumes a power law relationship
between 
and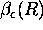 
(Klett (1981)):
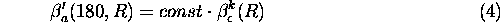
where k, which is generally in the interval
0.67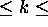 
1.0 (Klett (1981), p. 212), depends on both the lidar
wavelength and various aerosol properties which include the aerosol shape,
composition, and number distribution. The
power law relationship can be substituted into the differential form
of the logarithmic lidar equation:
where:
to get the following nonlinear ordinary differential equation:
This equation has the same form as the Bernoulli equation and is easily solved. If k is assumed to be a constant, then the solution to Equation 7 is:
where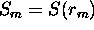 
and 
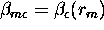(Klett (1981), p. 213). This solution assumes that the backscatter by the atmospheric
aerosols dominates the molecular backscatter. At 1064 nm, the wavelength of
the VIL, this assumption is valid and Equation 8 can be used
to solve the lidar equation. To maintain
the stability and accuracy of the solution,
Equation 8 has to be integrated backwards from far ranges.
The dependence of this form of the solution on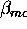 
decreases
with decreasing r.
Equation 1 can also be solved by using a calibration source. Previous studies have used the lidar signal above or below cirrus clouds as the calibration source. It has been assumed that the backscattered radiation at the chosen height was the result of only molecular scattering (Sassen (1989)). This method used a constant multiple scattering correction factor and made an additional assumption for a constant backscatter to extinction ratio for the cirrus particles. Uncertainties in this method are largely due to aerosols in the calibration layer which cause a larger than expected signal for the molecular backscatter. This leads to smaller than expected aerosol backscatter cross sections which cause underestimates in the cirrus cloud visible optical depth calculations.
For the two channel approach used by the HSRL, Equation 1 was separated into two equations: one for molecular backscatter and one for aerosol backscatter (Shipley et al. (1983)):
where:
where:
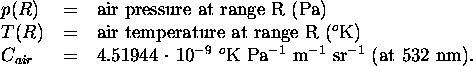
A rawinsonde profile gives the needed information to solve
Equation 11. Using the calculated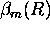 
at each range
(using Equation 3 and Equation 11),
can be determined by inverting Equation 9:
Equation 11 gives a calibrated target at every range. This calibration target can be used to solve for the aerosol backscatter cross section per unit volume by taking the ratio of the two scattering equations (Equation 9 and Equation 10) and rearranging terms:
If gaseous and particulate absorption are negligible (extinction is just a result of scattering processes) then the aerosol scattering cross section is:
{The integration of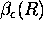 
with range determines the
aerosol visible optical depth (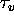
):
Knowledge of 
enables the calculation of the aerosol backscatter
phase function:
This set of equations shows the advantage of the HSRL over a single channel lidar system. The HSRL configuration allows for the direct calculation of the cirrus cloud visible optical depth, aerosol backscatter cross sections, and aerosol backscatter phase functions (if gaseous and particulate absorption are negligible).
