

Next: Structure Functions
Up: Horizontal Cirrus Cloud
Previous: Horizontal Cirrus Cloud
Return to the Publications.
Return to the Index.
Cirrus cloud cover percentages were calculated for the VIL simulated RTIs
and the HSRL RTI for the two time periods. To compare the VIL and HSRL
cloud cover percentage values, the HSRL data had to be shifted upwind to
the position where the same cirrus clouds occurred in the VIL scans. This time
shift ( 10 minutes) was used to match the two data sets. The shift was
determined from the distance between the two systems and the average
wind speed at the cirrus cloud heights. The average wind direction at
the cirrus cloud heights, determined by the rawinsonde, was
used to calculate the direction to shift the HSRL data upwind. The HSRL
shifted RTI and VIL simulated RTI cirrus cloud cover percentages
were then compared for the two data periods.
10 minutes) was used to match the two data sets. The shift was
determined from the distance between the two systems and the average
wind speed at the cirrus cloud heights. The average wind direction at
the cirrus cloud heights, determined by the rawinsonde, was
used to calculate the direction to shift the HSRL data upwind. The HSRL
shifted RTI and VIL simulated RTI cirrus cloud cover percentages
were then compared for the two data periods.
For the first time period (18:08-19:24 GMT), broken cirrus clouds
were advected into the region from 278 to 297
to 297 at wind speeds
ranging from 26 ms
at wind speeds
ranging from 26 ms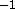 to 40 ms
to 40 ms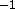 . Cirrus cloud cover percentages were
calculated for the 60 km of VIL vertical profiles spaced every 100 m
(Figure 3). The individual RTIs show cirrus
cloud cover percentages ranging from 54.7% 17.2 km south
of the VIL to 100% both directly above the VIL and 30 km to the north
of the VIL. The mean cloud cover was 81.5% for the mesoscale volume.
The maximum difference in cloud cover between two RTIs in the 60 km spread
was 45.3%. The maximum cloud cover difference between two RTIs
10 km apart was 27.8%. For the
same time period, the time shifted HSRL data had a cloud cover percentage
of 100%. Since the VIL along wind scan was not
perpendicular to the wind axis, the
cirrus clouds seen by the HSRL passed 5.54 km to the north of the VIL.
. Cirrus cloud cover percentages were
calculated for the 60 km of VIL vertical profiles spaced every 100 m
(Figure 3). The individual RTIs show cirrus
cloud cover percentages ranging from 54.7% 17.2 km south
of the VIL to 100% both directly above the VIL and 30 km to the north
of the VIL. The mean cloud cover was 81.5% for the mesoscale volume.
The maximum difference in cloud cover between two RTIs in the 60 km spread
was 45.3%. The maximum cloud cover difference between two RTIs
10 km apart was 27.8%. For the
same time period, the time shifted HSRL data had a cloud cover percentage
of 100%. Since the VIL along wind scan was not
perpendicular to the wind axis, the
cirrus clouds seen by the HSRL passed 5.54 km to the north of the VIL.
There are a couple of interesting features to note in
Figure 3. A cloud cover percentage of 100% was seen directly
above the VIL. This maximum was
the result of a very thin cirrus cloud layer located at a height of 10 km, the
tropopause. This high cloud cover percentage was the result of specular
reflection from ice crystals. Specular reflection
occurs when higher than normal signal is backscattered to the
receiver due to specific ice crystal orientations. When the cirrus
cloud ice crystals are in the form of plates they
can become positioned such that their flat surfaces are parallel to the ground.
This plate orientation causes enhanced laser backscatter when the lidar at
the ground is viewing vertically. Directly above
the VIL specular reflection occurred but the backscattered signal
off the vertical did not show this enhanced backscatter. This reveals the
importance of tilting the receiver of a vertically pointing lidar system
slightly off of the vertical. For this early time period, the HSRL
saw 100% cirrus cloud cover due to the oriented ice crystals.
The VIL also detected signal from this height but the backscatter
signal was smaller than the threshold value, causing the VIL to miss these
clouds (except for the cases where specular reflection occurred). During
this experiment, the HSRL was tilted off of the vertical to remove the
occurance of specular reflection. The 100% cirrus cloud cover percentage
seen by the HSRL shows that specular reflection was a problem and that the
HSRL receiver was not tilted as far off of the vertical as was originally
thought.
A second interesting feature in Figure 3 was the variation
of the cirrus clouds within the volume. By comparing the cirrus cloud
cover at 17.2 km and 24.7 km to
the south of the VIL, a cloud cover difference of 27.8% was seen.
This difference shows the variability of cirrus clouds across a short
distance (7.5 km) even when the cloud cover is averaged in time.
This cirrus cloud variability shows possible sampling errors when point
measurements are used to represent the cirrus cloud cover over an area.
A point measurement made at either 17.2 km or 24.7 km south of the VIL
could not accurately describe the general cirrus clouds structure within a
mesoscale volume. This reveals the difficulties encountered when using
a single vertically pointing system to describe the cirrus
cloud spatial structure over a large area.
The variation of cirrus clouds within a small region suggests a need to
view cirrus clouds throughout the mesoscale volume.
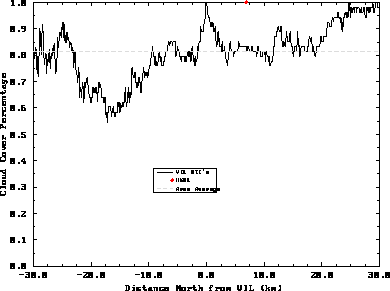
Figure 3: Cloud cover percentages calculated for 601 simulated RTIs for the
time period 18:08 to 19:24 GMT on December 1, 1989. The x-axis is the distance
from the VIL (north is positive).
The y-axis is the cloud cover percentage. The solid line is cloud cover
percentages for each VIL simulated RTI (consecutive RTIs are separated
by 100 meters). These cloud cover percentages are aligned along the wind
resulting in a time average of the cirrus clouds for each RTI.
The solid circle is the time shifted HSRL cloud cover percentage. The
dashed line is the average VIL cloud cover percentage for this time
period. Note the specular reflection directly above the VIL.
Since cirrus clouds affect the incoming solar radiation, an error
in the cirrus cloud cover percentage will result in changes in the
calculated visible radiative flux reaching the surface of the Earth.
The magnitude of the change in the calculated visible radiative flux
will determine whether the cirrus cloud cover needs to be considered when
discussing climate warming.
To estimate the magnitude of this change in the incoming solar flux,
consider a simple calculation for the change in the direct solar flux
due to an incorrect cirrus cloud cover percentage:

where:

On the right hand side of Equation 18, the first term
is the change in radiance produced from the transmission of the solar radiation
through the cloudless atmosphere while the second term
is the change in radiance error produced from the transmission of solar
radiation through the cirrus clouds. The absolute value was taken because
we are only interested in an estimate of the magnitude of the
change of the incoming solar radiation,
not whether warming or cooling would occur. For the Earth,
 is described as the following:
is described as the following:

where 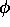 is the latitude and
is the latitude and  is the solar declination
angle which is defined as:
is the solar declination
angle which is defined as:

with 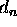 as the day of the year. The hour angle,
as the day of the year. The hour angle, 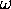 , is
defined as:
, is
defined as:

where H is number the of hours from local noon.
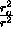 can be rewritten in the following form:
can be rewritten in the following form:
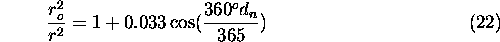
Equations 18 to 22 were used to estimate a change
in the direct visible radiative flux seen at the surface of the
earth due to an incorrect cirrus cloud cover. The cloud cover percentage error
used for the first time period was the difference between the
minimum and maximum VIL RTI cloud cover percentages. The HSRL cloud
cover percentage for the same cirrus cloud deck was not used because of possible
contamination by specular reflection. The absorption of solar
radiation by the atmospheric constituents was neglected in these
calculations. For the first time period, the transmissivity
of the cirrus clouds at solar wavelengths was defined by the cirrus cloud
visible optical depth measured by the HSRL, 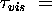 0.257.
0.257.
An estimate of the change in solar flux at the surface of the
earth for Madison, Wisconsin
at 13:00 GMT on December 1, 1989 was calculated using Equation 18.
For this time period, a 45.3% difference in cirrus cloud cover resulted
in a change of 58.18 Wm seen at the surface of the Earth. The
magnitude of this error was approximately 14 times greater than the effects
due to the doubling of CO
seen at the surface of the Earth. The
magnitude of this error was approximately 14 times greater than the effects
due to the doubling of CO , 4 Wm
, 4 Wm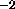 . Obviously an incorrect cloud cover
will have an important effect on both the radiative balances occurring in
the atmosphere and the models simulating the radiative and dynamical
structure of the Earth's atmosphere. Even
though Equation 18 does not incorporate the Earth's surface albedo or
absorption by atmospheric gases, it does show the need for the accurate
simulation of cirrus clouds and their global coverage.
. Obviously an incorrect cloud cover
will have an important effect on both the radiative balances occurring in
the atmosphere and the models simulating the radiative and dynamical
structure of the Earth's atmosphere. Even
though Equation 18 does not incorporate the Earth's surface albedo or
absorption by atmospheric gases, it does show the need for the accurate
simulation of cirrus clouds and their global coverage.
For the later time period (19:29 to 21:20 GMT), scattered cirrus clouds
were present until 20:30 when a widespread, three
kilometer thick, cirrus cloud
deck was advected into the region from approximately  . The
area averaged cloud cover for
the VIL was 76.8%, 4.7% smaller than the previous
time period. The HSRL cloud cover was 67.9% (Figure 4),
resulting in a cloud cover difference between the two systems of 8.9%. The
minimum cloud cover detected by a VIL RTI was 59.0%, from 0.7 to 1.0 km
north of the system. The
maximum detected cloud cover was 100%, 29.8 km to the north. A
maximum cloud cover difference of 41.0% was seen between the VIL RTIs.
The maximum cirrus cloud cover difference detected between RTIs
separated by 10 km was 30.8%.
Again large variations in the cloud cover were noticed depending on the
location of a vertically pointing lidar. Specular reflection does not have as
large of an effect on the cloud cover percentages
because most of the cirrus clouds were lower and optically thicker than the
previous time period. Also, the thin cirrus layer at the tropopause was not
detected after 20:00 GMT.
. The
area averaged cloud cover for
the VIL was 76.8%, 4.7% smaller than the previous
time period. The HSRL cloud cover was 67.9% (Figure 4),
resulting in a cloud cover difference between the two systems of 8.9%. The
minimum cloud cover detected by a VIL RTI was 59.0%, from 0.7 to 1.0 km
north of the system. The
maximum detected cloud cover was 100%, 29.8 km to the north. A
maximum cloud cover difference of 41.0% was seen between the VIL RTIs.
The maximum cirrus cloud cover difference detected between RTIs
separated by 10 km was 30.8%.
Again large variations in the cloud cover were noticed depending on the
location of a vertically pointing lidar. Specular reflection does not have as
large of an effect on the cloud cover percentages
because most of the cirrus clouds were lower and optically thicker than the
previous time period. Also, the thin cirrus layer at the tropopause was not
detected after 20:00 GMT.
By using Equation 18
for Madison, Wisconsin at 14:30 GMT on December 1, 1989, with an average
 0.428 for the cirrus clouds (measured by the HSRL),
a change of 12.36 Wm
0.428 for the cirrus clouds (measured by the HSRL),
a change of 12.36 Wm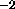 was seen at the surface of the
Earth. This value was approximately five times smaller than the previous time
period. The early time period had a large cloud cover difference
and small optical depth. The latter had a smaller cloud cover difference
and a larger optical depth. It also had less incident solar radiation
due to the time of day. There were compensating effects during the
second time period due to the larger optical depth and the smaller cloud cover
difference. The larger cirrus cloud optical depth reduced the incoming
solar radiation more than the earlier time period but the smaller
cirrus cloud cover percentage difference
decreased the effect of the cirrus clouds on the radiation balance.
The change in the radiative
flux caused by cirrus clouds for either time period would dominate the
atmospheric temperature increases caused by the doubling of CO
was seen at the surface of the
Earth. This value was approximately five times smaller than the previous time
period. The early time period had a large cloud cover difference
and small optical depth. The latter had a smaller cloud cover difference
and a larger optical depth. It also had less incident solar radiation
due to the time of day. There were compensating effects during the
second time period due to the larger optical depth and the smaller cloud cover
difference. The larger cirrus cloud optical depth reduced the incoming
solar radiation more than the earlier time period but the smaller
cirrus cloud cover percentage difference
decreased the effect of the cirrus clouds on the radiation balance.
The change in the radiative
flux caused by cirrus clouds for either time period would dominate the
atmospheric temperature increases caused by the doubling of CO . This
implies that knowledge of the spatial structure is very important in
understanding the radiative effects of cirrus clouds on the climate.
. This
implies that knowledge of the spatial structure is very important in
understanding the radiative effects of cirrus clouds on the climate.
As was previously shown, cirrus clouds can vary significantly over a
mesoscale area. Very precise
point measurements of cirrus clouds will not give reliable statistics of
the cirrus clouds due to the cloud sampling errors. Better instruments
which only measure a vertical profile through the atmosphere
would not be able to accurately describe the influence of the cirrus cloud
spatial structure on the climate because of the sampling
errors. Even a very long time
average would not give an accurate description of the cirrus clouds. The
long time average would be biased because the clouds have to be advected over
the instrument. The cross wind cirrus cloud variation would not be detected,
and, as shown previously, this can be significant (especially if the cirrus
clouds tend to align along the wind direction).
Although the VIL has been used to determine the cirrus cloud spatial structure
throughout a mesoscale volume, the effects of this cirrus cloud variation
on the Earth's radiation balance has yet to be determined.
In some models which simulate the effects of cirrus clouds on the Earth's
radiation balance, the three dimensional cirrus clouds
have been averaged to produce a cirrus cloud layer with the equivalent
radiative properties, an `equivalent uniform layer'. This reduction in
complexity of the cirrus cloud radiative properties can be achieved for
the radiative effects of the cirrus clouds at one wavelength of
radiation according to the mean value theorem. Complexities arise in
this process when the radiative effects
of the cirrus clouds has to be described at two different wavelengths, say
at both visible and infrared wavelengths. In this case, the
radiative effects at both wavelengths have to be matched within the equivalent
uniform layer of cirrus clouds, which may not be possible.
Even if an equivalent uniform layer was used, the radiative properties
of the cirrus clouds may be reproduced but the
dynamical structure of the atmosphere would not be reproduced. Since
clouds are an integral part of the atmosphere they affect both the
radiative balance and the dynamical structure. An equivalent uniform
cloud field will not have the same dynamical effect as multi-layered
scattered cirrus cloud field. As an example,
if a previously uniform cirrus cloud field was evaporating and
breaking up, then there would be
regions of subsidence within the cloud field. This will not be simulated in
a model using an equivalent uniform layer as a parameterization
for cirrus clouds.
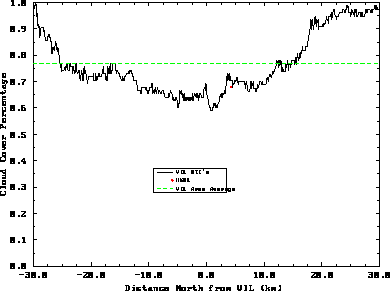
Figure 4: Same as Figure 3 except for the time period from 19:29 to 21:20 GMT on
December 1, 1989.


Next: Structure Functions
Up: Horizontal Cirrus Cloud
Previous: Horizontal Cirrus Cloud
Return to the Publications.
Return to the Index.
Antti Piironen
Thu Apr 11 08:27:54 CDT 1996
 10 minutes) was used to match the two data sets. The shift was
determined from the distance between the two systems and the average
wind speed at the cirrus cloud heights. The average wind direction at
the cirrus cloud heights, determined by the rawinsonde, was
used to calculate the direction to shift the HSRL data upwind. The HSRL
shifted RTI and VIL simulated RTI cirrus cloud cover percentages
were then compared for the two data periods.
10 minutes) was used to match the two data sets. The shift was
determined from the distance between the two systems and the average
wind speed at the cirrus cloud heights. The average wind direction at
the cirrus cloud heights, determined by the rawinsonde, was
used to calculate the direction to shift the HSRL data upwind. The HSRL
shifted RTI and VIL simulated RTI cirrus cloud cover percentages
were then compared for the two data periods.


 to 297
to 297 at wind speeds
ranging from 26 ms
at wind speeds
ranging from 26 ms to 40 ms
to 40 ms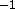 . Cirrus cloud cover percentages were
calculated for the 60 km of VIL vertical profiles spaced every 100 m
(Figure
. Cirrus cloud cover percentages were
calculated for the 60 km of VIL vertical profiles spaced every 100 m
(Figure 


 is described as the following:
is described as the following:

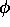 is the latitude and
is the latitude and  is the solar declination
angle which is defined as:
is the solar declination
angle which is defined as:

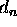 as the day of the year. The hour angle,
as the day of the year. The hour angle, 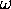 , is
defined as:
, is
defined as:

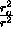 can be rewritten in the following form:
can be rewritten in the following form:
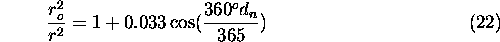
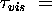 0.257.
0.257.
 seen at the surface of the Earth. The
magnitude of this error was approximately 14 times greater than the effects
due to the doubling of CO
seen at the surface of the Earth. The
magnitude of this error was approximately 14 times greater than the effects
due to the doubling of CO , 4 Wm
, 4 Wm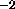 . Obviously an incorrect cloud cover
will have an important effect on both the radiative balances occurring in
the atmosphere and the models simulating the radiative and dynamical
structure of the Earth's atmosphere. Even
though Equation
. Obviously an incorrect cloud cover
will have an important effect on both the radiative balances occurring in
the atmosphere and the models simulating the radiative and dynamical
structure of the Earth's atmosphere. Even
though Equation  . The
area averaged cloud cover for
the VIL was 76.8%, 4.7% smaller than the previous
time period. The HSRL cloud cover was 67.9% (Figure
. The
area averaged cloud cover for
the VIL was 76.8%, 4.7% smaller than the previous
time period. The HSRL cloud cover was 67.9% (Figure  0.428 for the cirrus clouds (measured by the HSRL),
a change of 12.36 Wm
0.428 for the cirrus clouds (measured by the HSRL),
a change of 12.36 Wm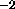 was seen at the surface of the
Earth. This value was approximately five times smaller than the previous time
period. The early time period had a large cloud cover difference
and small optical depth. The latter had a smaller cloud cover difference
and a larger optical depth. It also had less incident solar radiation
due to the time of day. There were compensating effects during the
second time period due to the larger optical depth and the smaller cloud cover
difference. The larger cirrus cloud optical depth reduced the incoming
solar radiation more than the earlier time period but the smaller
cirrus cloud cover percentage difference
decreased the effect of the cirrus clouds on the radiation balance.
The change in the radiative
flux caused by cirrus clouds for either time period would dominate the
atmospheric temperature increases caused by the doubling of CO
was seen at the surface of the
Earth. This value was approximately five times smaller than the previous time
period. The early time period had a large cloud cover difference
and small optical depth. The latter had a smaller cloud cover difference
and a larger optical depth. It also had less incident solar radiation
due to the time of day. There were compensating effects during the
second time period due to the larger optical depth and the smaller cloud cover
difference. The larger cirrus cloud optical depth reduced the incoming
solar radiation more than the earlier time period but the smaller
cirrus cloud cover percentage difference
decreased the effect of the cirrus clouds on the radiation balance.
The change in the radiative
flux caused by cirrus clouds for either time period would dominate the
atmospheric temperature increases caused by the doubling of CO . This
implies that knowledge of the spatial structure is very important in
understanding the radiative effects of cirrus clouds on the climate.
. This
implies that knowledge of the spatial structure is very important in
understanding the radiative effects of cirrus clouds on the climate.
