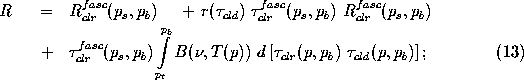
Return to the Publications.
Return to the Index.
where the radiance contribution above the cloud was shown to be negligible by the FASCOD3P model, the upwelling model radiance includes the terrestrial contribution, the model derived radiances are corrected based on Equation 8, and the spectral dependence is implied. Rearranging terms results in a radiance value that effectively projects the instrument to cloud base:

Integration by parts transforms the right hand side, such that
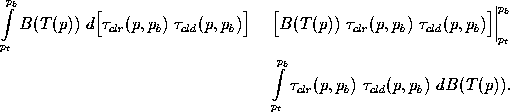
The Trapezoid Rule is applied to the remaining integral at the endpoints to obtain a final solution for the cloud transmissivity
where

is the downwelling cloud radiance; and
![]()
is the average Planck radiance of the cloud determined from local
radiosonde data and lidar derived cloud boundaries, and
the clear sky transmissivity within the cloud, ![]() , is obtained from FASCOD3P. The solution is
iterated for
, is obtained from FASCOD3P. The solution is
iterated for ![]() in the reflectance term until a solution
converges to within 0.001 (Ackerman et al., 1990).
in the reflectance term until a solution
converges to within 0.001 (Ackerman et al., 1990).
The algorithm takes into consideration the fact that the cloud may be
opaque. This reduces the effective cloud top altitude, while
increasing the effective cloud top temperature.
Equation 15 would yield an unphysical solution
based on true cloud base and top temperatures. Therefore,
a direct solution of Equation 15 is
not attempted because the measured radiance for an opaque cloud
will be larger than the mid-cloud radiance determined from radiosonde
measurements. The result is a ![]() :
: ![]() ratio
that becomes larger than unity, yielding a negative,
unphysical solution of Equation 15.
ratio
that becomes larger than unity, yielding a negative,
unphysical solution of Equation 15.
Instead, the cloud is broken into vertical layers defined by the radiosonde temperature profile, where the cloud transmittance is calculated from the cloud base to a given altitude layer. If the transmittance becomes negative, the cloud is labeled as opaque at the previous altitude. Otherwise, the process continues until the cloud top is reached, where the solution is taken to be the cloud infrared transmittance. It will be shown that a cloud transmittance less than 0.05 (infrared optical depth > 3) is the minimum resolvable value.