Return to the Publications. Return to the Index.

AERI and HSRL Derived Brightness Temperature

 
AERI measured atmospheric column radiance is converted to brightness temperature at each microwindow using Equation 4. This data serves as a reference for HSRL calculated brightness temperature, derived using the visible column optical depth. The HSRL vertical optical depth profile can be converted to an infrared value based on either the ratio data given in Table 4 or the theoretical values derived from Mie theory. A radiosonde profile provides the vertical temperature structure necessary to calculate the Planck radiance at each atmospheric layer. Clear sky radiance and transmissivity calculated with FASCOD3P for the optical depth inversion is used to determine the molecular radiance contribution; which is added to the product of the clear sky transmissivity and the HSRL derived cloud radiance to determine the total column radiance at the given wavenumber. The model derived radiance is adjusted using the Gamma correction to account for errors in the water vapor continuum. This column radiance is then converted to brightness temperature for a spectral comparison with the AERI. The results will be presented in a form similar to the last section: data for a single case and as a scatter plot comprising the entire cirrus data set.

Data given in Figure 22 showed that the least particle size dependent microwindow, for ice spheres, is near 920 cm. Therefore, one would expect HSRL derived brightness temperatures to agree with AERI measured values near this region, and exhibit a decrease in correlation away from this region. This should be more apparent within the microwindows located above 1000 cm, where the absorption is weak and more sensitive to particle size. Four microwindows have been chosen for this comparison: a pair of strong absorption regions at 811 and 820 cm; the cross-over point at 934 cm; and a weak absorption region at 1096 cm.

Figure 23 illustrates the HSRL derived brightness temperature (dashed lines) relative to AERI data (solid lines) for the strong absorption regions located at 811 cm (upper) and 820 (lower) cm on 17 November 1994. The results are based on the Mie calculated optical depth ratios in Figure 22. The shaded region within the dashed lines accounts for the difference between 25 and 100 m particles. The HSRL derived 820 cm microwindow shows similar agreement with AERI measurements as the 811 cm microwindow, while demonstrating an opposite bias from the baseline temperature. Figure 22 shows similar disagreement between the 811 and 820 cm visible to infrared OD ratios, where the 811 cm experimental results appear to disagree with the trend demonstrated by the other data.

  
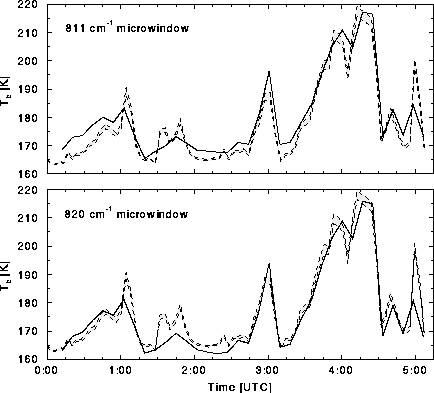
Figure 23: HSRL derived brightness temperature (dashed lines) relative to AERI measured values (solid lines) for 811 cm (upper) and 820 cm (lower) microwindows on 17 November 1994, Madison. The shaded regions between the dashed lines represents the shift in derived brightness temperature due to a change from 25 to 100 m particle sizes.

Figure 24 is similar to Figure 23 but illustrates results for the 934 cm (upper) and 1096 cm (lower) microwindows on 17 November 1994. The deviation in expected brightness temperature is minimal at 934 cm, whereas the 1096 cm microwindow exhibits a large dependence on particle size. This is consistent with the Mie calculations shown in Figure 22. HSRL derived brightness temperatures are also in close agreement within these microwindows. The largest discrepancies in the data (near 01:45, 03:00 and 05:00 UTC) are due to the instrumental characteristics discussed in Section 4.1. This particular case was favorable because the clouds never become opaque.

  
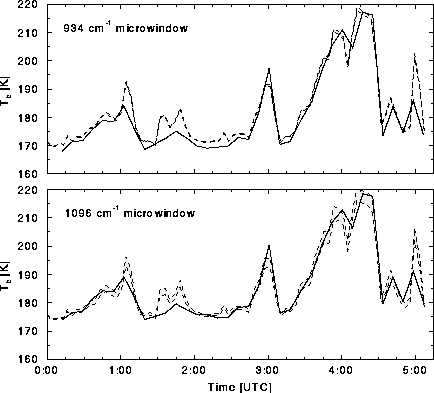
Figure 24: HSRL derived brightness temperature (dashed lines) relative to AERI measured values (solid lines) for 934 cm (upper) and 1096 (lower) microwindows on 17 November 1994, Madison. The shaded regions between the dashed lines represents the shift in derived brightness temperature due to a change from 25 to 100 m particle sizes. Both regions compare well with AERI measured results. Note the reduced uncertainty in the 934 cm microwindow as a function of particle size. This is consistent with the analysis of Figure 22.

The case of 9-10 November 1995 did become opaque, between 2:30 and 3:30 UTC. This is apparent in Figures 12 and 15. Brightness temperature data for the 934 cm microwindow is given in Figure 25, shown relative to the HSRL measured optical depth (bottom). The two instruments exhibit good correlation until 2:30 UTC, where the cirrus becomes opaque (shaded region).

  
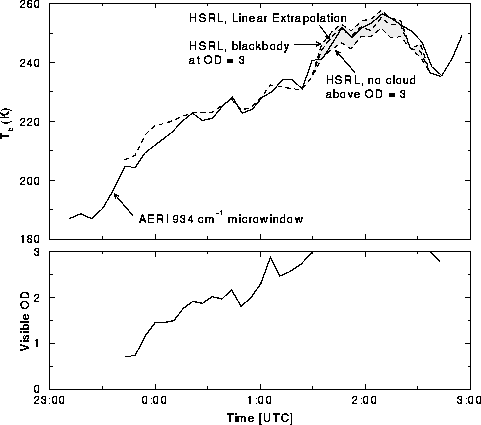
Figure 25: Upper figure shows HSRL derived brightness temperature as a function of time at 934 cm (dashed line) relative to AERI measured values (solid) on 9-10 November 1995 at Madison. Shaded portion of figure represents an HSRL observed opaque cloud. Lower figure illustrates HSRL measured visible column optical depth.

Calculation of vertically integrated radiance is performed until the cloud becomes opaque. The visible optical depth above this altitude must be approximated to continue calculation of the column integrated radiance. Three values are determined for this region: a minimum radiance, assuming the cloud terminates where it becomes opaque; a linearly extrapolated value, continuing the calculation based on the change in optical depth over the last 1 km; and a maximum radiance, assuming a blackbody emitter above the opaque point. The AERI measured data shows better agreement when the data is extrapolated, Figure 25.

HSRL and AERI brightness temperature calculations show good correlation over a 100 K temperature range. Figure 26 illustrates data from all cirrus cases for the 934 cm microwindow, where HSRL data was interpolated to coincide with AERI times. The dashed lines represent a 5 K deviation from perfect correlation between the instruments. All data points are shown, including those that required extrapolation due to opaque cloud cover. The upward trend in the data is a result of the linear extrapolation of HSRL optical depth when the cloud becomes opaque, which tends to underestimate the optical depth and, therefore, the derived brightness temperature relative to the AERI measured values.

  
Figure 26: AERI and HSRL derived brightness temperature data for the cirrus cases given in Table 3 for the 934 cm microwindow. Dashed lines represent 5 K deviation from perfectly correlated instrument data.

HSRL derived radiance can be utilized to determine a weighted visible to infrared optical depth ratio, . This is accomplished by iterating , Section 2.2.4, until the HSRL derived radiance agrees with AERI measured values to within 0.001 mW (m  sr cm), rather than using derived in Section 4.1. This should yield an improvement relative to the results determined in Section 4.1, which were based on a direct ratio of HSRL measured visible to AERI derived infrared optical depth. The previous approach assumes a uniform cloud extinction cross-section to determine the IR optical depth. This method inherently weights the cloud extinction cross-section, given the HSRL vertical resolution. Figure 27 illustrates the values of derived for all spectral microwindow regions for the data cases given in Table 3.

  
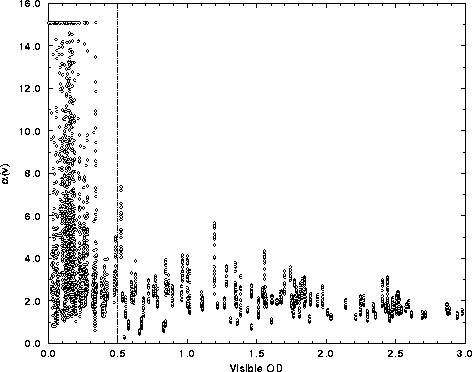
Figure 27: Visible to infrared optical depth ratio, , comprising all spectral microwindows for the data cases listed in Table 3. Regions of small optical depth (visible OD < 0.5) yield large uncertainties in due to ill conditioned solutions. Additional errors result from instrument field of view differences. The dashed line represents a constraint on the data which was used to derive the final value of .

Errors in determining are reduced by constraining the data. An upper limit of 15.0 is placed on the iteration, due to inconsistencies between the instruments for small optical depths. Data with a visible optical depth less than 0.5 are removed from the analysis, shown by the dashed line in Figure 27. Instrument field of view differences also yield discrepancies in some of the data. This is apparent when the cloud cover within the field of view is not uniform, Figure 28, resulting in the spatial averaging problems discussed in Section 4.1. When this occurs the HSRL derived column radiance does not correlate with AERI data, resulting in a non-physical visible to infrared optical depth ratio. Small breaks in near-uniform cloud cover often underestimate ; whereas spatially-small, optically-thick clouds in an otherwise clear sky overestimate . This is a result of the large AERI field of view relative to the HSRL.

  
Figure 28: Visible to infrared optical depth ratio, , (upper curve) as a function of time, relative to the visible optical depth (lower curve), at 934 cm  for 17 November 1994 data.

Figure 28 shows the variation in (934 cm) as a function of time for data acquired on 17 November 1994. The lower figure illustrates the HSRL measured visible optical depth which was used to derive the values in the upper figure. The regions of increased slope in the lower figure represent temporal changes within the HSRL field of view. The larger AERI field of view and increased dwell time yield radiance measurements that will differ from HSRL derived values. Cases with increased spatial uniformity (e.g., 10 November 1995) will produce reduced scatter in the data, increasing the number of available data points for an improvement in the final statistical analysis. This is evident in Figure 29, which contrasts the results of 17 November 1994 against the other cases.

  
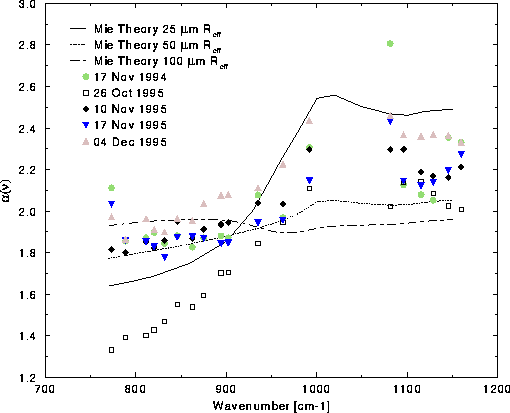
Figure 29: Spectral visible to infrared optical depth data for individual data cases listed in Table 3. The cases that are not shown did not have data within the constraints given in Figure 27. Data from 26 October 1995 appears to be underestimated due to the presence of opaque, low-altitude mixed phase clouds.

A spectral comparison of data for individual cases is given in Figure 29 relative to Mie theory. Three of the eight cases listed in Table 3 are not shown because data did not include visible optical depths greater than 0.5 during the data acquisition period. The results from 17 November 1994 (green circles) in Figure 29, exhibited the largest scatter of the cases shown. This was expected given the non-uniformity in cloud cover, and optical depth, indicated in Figure 28. The anomalous 26 October 1995 data (open squares), where appears to be underestimated between 750 and 900 cm, is likely due to the HSRL telescope configuration which has its focus at infinity. This yields an overlap region between the transmitter and receiver for the first 2.5 km from the surface. The 26 October 1995 case consisted of optically thick ice and mixed phase clouds (shown by HSRL), with a cloud base altitude that varied between 2 and 4 km, which became opaque to the HSRL. This resulted in a visible optical depth measurement that was less than expected, which underestimated the visible to optical depth ratio. The HSRL is capable of such measurements if a refocusing lens is placed in the telescope. This will effectively reduce the receiver and transmitter overlap region. The remaining cases show good agreement relative to one another. Note that the least scatter in the data among all spectral regions occurs at 934 cm. However, all spectral regions exhibiting strong absorption (below 1000 cm) show minimal scatter, aside from the anomalous 04 December 1995 case.

Figure 29 illustrates that experimental values of for the individual data cases are consistent with Mie theory for 50 to 100 m radius particles for wavenumbers smaller than 900 cm, but consistent with 25 to 50 m radius particles for wavenumbers larger than 900 cm. This suggests that the entire experimental curve is biased toward larger values of . Analysis of Equation 31 indicates that there are five possible explanations for the apparent bias: HSRL measured cloud visible optical depth was overestimated; FASCOD3P calculated clear sky radiance was overestimated; AERI measured downwelling column radiance was overestimated; field of view differences between the instruments yield uncorrelated observations; or limitations of Mie assumptions. The last factor is expected to be negligible in all but specific cases (e.g., a given orientation of ice crystals).

The first three possibilities are inconsistent with instrumental characteristics and measured results. Figure 18 demonstrated HSRL measurement errors due to multiply-scattered return within the HSRL field of view. However, this effect would yield a larger than expected return signal, which corresponds to an underestimate in the measured visible optical depth. FASCOD3P calculations within the microwindow regions also underestimate the radiance relative to AERI measured values, and the Gamma correction minimizes the model errors. The small uncertainty in the AERI measurements eliminates the third possibility.

The bias in the results was likely due to AERI and HSRL instrumental differences. Field of view differences between the instruments were shown to account for large errors during non-uniform cloud cover cases. One would expect the field of view differences to average over a large data set. However, this is not possible given the data analysis constraint imposed on data with a visible optical depth less than 0.5. For cases where the HSRL field of view is full and the AERI FOV is partially clear, is overestimated because the AERI measured radiance is less than the HSRL derived radiance. Cases where the HSRL FOV observes a clear data point while the AERI FOV is partially clear would be ignored because the visible optical depth value is less than 0.5. The spectral bias in is quite apparent when combining all data points, Figure 30.

  
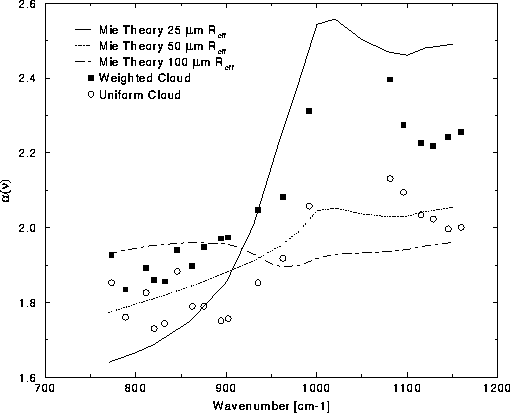
Figure 30: Similar to Figure 22, but updated with using weighted data from all cases. The weighted data (solid squares) produces values that are more consistent with the Mie theory results. The data implies an average radius of about 35 m, assuming spherical particles. Individual spectral results for the experimental data are given in Tables 4 and 5.

The data from all cases, except 26 October 1995, were combined to determine the effectiveness of iterating from a weighted cloud distribution, relative to the uniform cloud solution, and compared to Mie theory. The weighted results are shown in Figure 30 (solid squares) and demonstrate less scatter than the unweighted results (open circles). The weighted results are also more consistent with the Mie theory calculations, indicating a mean particle effective radius of roughly 35 to 40 m, assuming spherical particles. Table 5 lists for the weighted cloud experimental solutions for each of the microwindow regions.  

 

773.12
788.55
811.21
820.13
831.70
845.69
862.32
875.10
894.14
902.10 1.7396
1.6888
1.7337
1.7189
1.7263
1.8035
1.7759
1.8292
1.8774
1.8805 934.88
962.37
991.78
1080.97
1095.68
1115.21
1128.71
1145.34
1159.56 1.9731
2.0332
2.2421
2.2804
2.2210
2.1915
2.1730
2.1738
2.1762

It is necessary to stress the importance of the Gamma correction on the data in the previous figures. The downwelling atmospheric column radiance within a microwindow, given optically thin cirrus or clear conditions, is small relative to optically thick cirrus. As a result, the FASCOD3P calculated radiance from below the cloud dominates the HSRL derived radiance from within the cloud for optically thin or clear conditions. The disagreement between AERI measured radiance and FASCOD3P calculated radiance is significant for these cases. The Gamma technique, detailed in Section 2.1.2, accounts for the difference between AERI and FASCOD3P radiances under clear conditions to correct this problem for all conditions. Figure 31 illustrates the relative radiance difference and absolute brightness temperature difference due to the Gamma correction for 17 November 1994 data This is shown as a function of time given a variable, HSRL measured, visible optical depth.

  
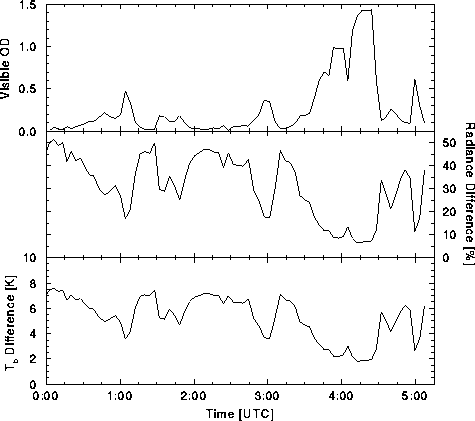
Figure 31: Effects of Gamma correction on HSRL derived brightness temperature for 17 November 1994 data. The upper curve illustrates the HSRL measured visible optical depth. The middle curve shows the contribution of FASCOD3P calculated clear sky radiance relative to the total column. The lower curve gives the absolute difference in brightness temperature that would result without without the use of the Gamma correction. The radiance and brightness temperature curves are for the 1096 cm microwindow.

The upper curve in Figure 31 indicates the HSRL measured visible optical depth as a function of time. This demonstrates the magnitude of error for optically thin relative to optically thick cirrus. Note that the Gamma corrected radiance, middle curve, can contribute as much as 50 percent of the total column radiance. That implies that the AERI measured clear sky radiance and FASCOD3P calculated clear sky radiance differ by two fold. Although the absolute radiance difference is small, the effect is large for optically thin cirrus or clear conditions. The total difference in HSRL derived brightness temperature is given in the lower curve of Figure 31, resulting in over 7 K difference for clear sky conditions. The radiance and brightness temperature differences are given for the 1096 cm microwindow region.

The errors associated with the brightness temperature calculations are similar to those for the optical depth inversions given in Section 4.1. The remainder of this section will detail the magnitude of expected error given the FASCOD3P uncertainties shown in Figure 20. Figure 32 illustrates the FASCOD3P derived clear sky radiance relative to HSRL derived column radiance within the 934 cm microwindow for data acquired on 9-10 November 1995. The model clear sky radiance contributes up to 50 percent of the total derived radiance for optically thin cirrus conditions prior to 00:00 UTC. Note that the AERI measured clear sky column radiance near 23:30 UTC is similar to the FASCOD3P calculated values, as expected.

  
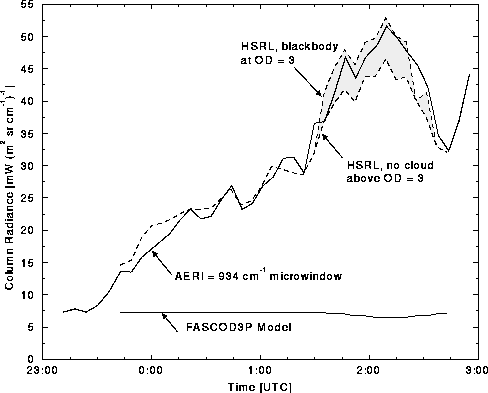
Figure 32: Comparison of measured and derived radiances for 9-10 November 1995. FASCOD3P contribution is shown to gauge the magnitude of clear sky radiance relative to cloud values. The decrease in FASCOD3P calculated radiance occurs with the decrease in cloud base altitude. HSRL derived values are indicated by the dashed lines, where the shading depicts opaque cloud cover.

Figure 33 shows the HSRL derived brightness temperature and expected error corresponding to the measured radiance and expected error given in Figure 20. The data corresponds to an HSRL measured visible optical depth of 0.5 for data acquired on 17 November 1994. The upper figure gives the HSRL measured brightness temperature (lower curve) and maximum expected brightness temperature (upper curve) based on FASCOD3P calculations derived from radiosonde uncertainties. The lower figure illustrates the absolute brightness temperature difference of the upper figure. This further suggests the importance of FASCOD3P calculations and radiosonde uncertainties to the final data products.

  
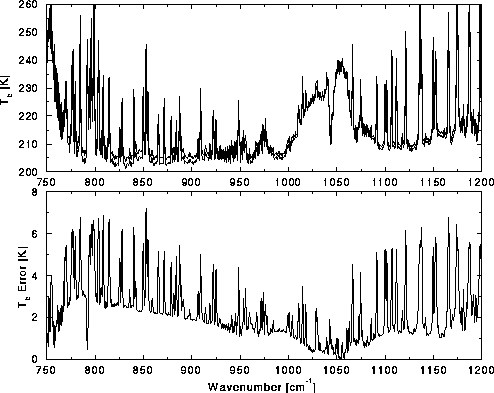
Figure 33: Upper figure shows HSRL derived brightness temperature (lower line) and maximum expected brightness temperature (upper line), given the radiance errors illustrated in Figure 20, for data acquired on 17 November 1994. The lower figure gives the absolute brightness temperature difference for the values shown in the upper figure. The resultant error is calculated for an AERI measured IR optical depth of 0.5