


Next: Convective Boundary Layer
Up: Methods for Determining
Previous: Methods for Determining
Return to the Publications.
Return to the Index.
The fair-weather convective boundary layer is
characterized by rising thermals of aerosol-rich air
and sinking streams of clearer air.
These vertical motions cause irregularities of the boundary layer top
which can be observed from the RHI scans of the VIL (see Figure 4).
When sampling the undulating boundary layer top with a traditional
point measuring probe, the measurements may be done through a
plume top or down-welling air parcel.
The vertical distance between the highest plume tops
and lowest parts of the down-welling free air may exceed the
boundary layer mean depth.
Nelson et. al
[41]
have measured entrainment zone
thicknesses ranging from 0.2 to 1.3 times the CBL mean depth.
This means in extreme cases that single point measurements of the CBL depth
may have more than 100% variations between individual observations.
To obtain a representative CBL depth estimate,
a long time (or line) averaging must be applied.
A traditional vertically pointing lidar offers
an improvement to the averaging problem,
since it can make continuous observations in one direction.
The CBL top is typically marked with a sudden backscatter intensity
change due to different aerosol concentrations in and above
the convective boundary layer.
Thus, the CBL top is usually determined from the first
sudden downhill gradient.
Determining the CBL depth in this manner
is not always a straightforward task.
A low contrast region may easily be interpreted as a part of the CBL.
This may lead to upward biased estimates early in the morning and
late afternoon
[55].
In addition, the sampling coverage of a vertically pointing lidar depends
on the time required for a thermal structure to drift over the lidar.
With a 5 ms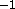 wind speed and a 1 km horizontal
scale of thermals, a vertically pointing lidar
samples across one thermal plume about every six minutes.
An integration over several plume passes is usually
required for obtaining statistically meaningful CBL depth estimates.
When measuring a rapidly growing CBL with a vertically pointing lidar,
averaging times cannot be extended
long enough to dampen the statistical fluctuations without
losing information about sudden changes in the CBL depth.
wind speed and a 1 km horizontal
scale of thermals, a vertically pointing lidar
samples across one thermal plume about every six minutes.
An integration over several plume passes is usually
required for obtaining statistically meaningful CBL depth estimates.
When measuring a rapidly growing CBL with a vertically pointing lidar,
averaging times cannot be extended
long enough to dampen the statistical fluctuations without
losing information about sudden changes in the CBL depth.
In contrast to the vertically pointing lidar,
the VIL scans about a 100 km volume
in three minutes, covering typically 10--50 thermal plumes.
Thus, the VIL volume scan
provides similar statistical properties in three minutes
as a vertically pointing lidar does after several hours of averaging.
Furthermore, the scan coverage does not significantly depend on the wind.
Although the CBL depth can be determined
from individual backscatter profiles of the VIL,
the angular scanning enables conversion of the data into more
informative RHI scans.
Then, the CBL structure can be observed by a visual inspection of
the RHI scans providing line averaged measurements
[56].
volume
in three minutes, covering typically 10--50 thermal plumes.
Thus, the VIL volume scan
provides similar statistical properties in three minutes
as a vertically pointing lidar does after several hours of averaging.
Furthermore, the scan coverage does not significantly depend on the wind.
Although the CBL depth can be determined
from individual backscatter profiles of the VIL,
the angular scanning enables conversion of the data into more
informative RHI scans.
Then, the CBL structure can be observed by a visual inspection of
the RHI scans providing line averaged measurements
[56].
When visually estimating the CBL mean depth from the RHI scans in this study,
the procedure of Boers et al.
[57]
is used.
The CBL mean depth definition is
adopted from Deardorff et al.
[58]:
the altitude which has equal areas of clear air below
and boundary layer aerosols above.
For example, the CBL depth is about 800 m
in the RHI scan shown in Figure 4.
The RHI scans have two advantages compared to point measurements.
First, an RHI scan makes it possible to visually distinguish between
aerosol layers above the CBL and thermal plumes connected to the ground.
This reduces the bias problems discussed above
in the case of interpretation of backscatter signals of
a vertically pointing lidar.
Second, an RHI scan provides better statistical properties than
a vertically pointing lidar or point measuring system.
A typical RHI scan of the VIL shows a 15 km long and 15 high
vertical cross section of the CBL.
When a vertically pointing lidar is used to obtain similar spatial
coverage, a one-hour observation time is required in
5 ms
high
vertical cross section of the CBL.
When a vertically pointing lidar is used to obtain similar spatial
coverage, a one-hour observation time is required in
5 ms wind.
wind.
In automatic estimation, the CBL mean depth is determined from the
horizontal signal variance
[40].
The horizontal aerosol variations are intense
at the altitude of the CBL mean depth, due to undulations
of the top of the CBL.
This also causes strong horizontal variations in the backscatter signal
at that altitude.
Thus, the horizontal signal variance has a maximum at the CBL mean depth.
This method was first used by Hooper and Eloranta
with the data obtained with an elevational scanning lidar[40].
This study follows the original method, but
a new calculation of vertical profile of horizontal signal variance and
an automatic interpretation scheme of the variance profiles are developed
to customize the method for the VIL data.
To calculate the vertical profile of horizontal signal variations,
each shot in a volume scan is first high-pass filtered with a
1 km long median filter.
This eliminates atmospheric extinction and scattering from uniformly
distributed aerosols, which do not provide
information about aerosol variations.
Using 20 m vertical (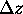 ) and 50 m horizontal spacings,
backscatter signals are mapped on
horizontal Constant Altitude Plan Position Indicator (CAPPI) planes.
Section 4.1 describes the mapping procedure.
The variance of each CAPPI plane is calculated and a
variance profile is formed.
) and 50 m horizontal spacings,
backscatter signals are mapped on
horizontal Constant Altitude Plan Position Indicator (CAPPI) planes.
Section 4.1 describes the mapping procedure.
The variance of each CAPPI plane is calculated and a
variance profile is formed.
The lowest-altitude local maximum of the variance profile that is
larger than the average of the profile marks the convective boundary
layer mean depth.
The bottom-up approach eliminates errors due to
strong aerosol variability caused by possible aerosol layers above the CBL.
Local maxima induced by dust clouds cause generally smaller variance
than the average of the signal variance profile.
Therefore, these maxima are rejected by requiring the
maximum peak to be stronger than the average of the variance profile.
Random variance fluctuations due to signal noise disturb
the detection of maximum
variance when the difference in backscatter from boundary layer aerosols and
free air is small.
To prevent selection of a random local maximum,
the points on either side of the maximum point
must be smaller than the maximum and larger than the next closest points,
i.e. 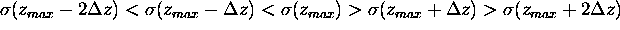 .
Figure 5 illustrates the selection criteria
of the maximum peak.
.
Figure 5 illustrates the selection criteria
of the maximum peak.
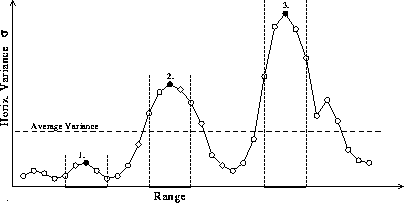
Figure 5: Schematic of the selection criteria.
Numbers 1-3 show local maximum peaks which satisfy
the criterion
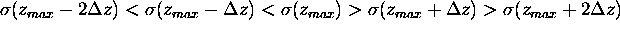 ;
vertical dashed lines highlight the region from
;
vertical dashed lines highlight the region from
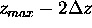 to
to 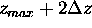 .
Noise-induced variance peaks remain below the average threshold limit.
In this case, peak 2 is selected, since it is the
first peak stronger than the average of the variance profile.
.
Noise-induced variance peaks remain below the average threshold limit.
In this case, peak 2 is selected, since it is the
first peak stronger than the average of the variance profile.
The automatic method provides a convective boundary layer mean depth
estimate representing an area-average over 70 km .
It is tested by comparing the mean depths with
manually inspected estimates.
Figure 6 shows an RHI scan, the VIL signal
variance profile, and the CBL mean depth estimated from the RHI scan.
The manual estimation is performed by visually inspecting
the altitude, which has equal areas of
boundary layer aerosols above and sinking air below from the RHI scan.
The figure shows a nearly perfect match between the variance profile
maximum and the manually estimated CBL mean depth.
.
It is tested by comparing the mean depths with
manually inspected estimates.
Figure 6 shows an RHI scan, the VIL signal
variance profile, and the CBL mean depth estimated from the RHI scan.
The manual estimation is performed by visually inspecting
the altitude, which has equal areas of
boundary layer aerosols above and sinking air below from the RHI scan.
The figure shows a nearly perfect match between the variance profile
maximum and the manually estimated CBL mean depth.

Figure 6: An RHI scan, the variance of the
filtered backscatter signal as a function of altitude (white curve),
and the convective boundary layer mean depth estimate
(black dashed line) on August 9, 1989, at 11:03 CDT.
Aerosol structures are shown as brighter areas; cleaner air
penetrating from free atmosphere is darker.
The CBL top undulations are clearly visible.
Figure 7 compares manually and automatically determined
convective boundary layer mean depths and estimates
from radiosonde-based potential temperature and specific humidity profiles
on July 28, 1989, from 8:00 to 10:00 CDT.
Because of the large number of RHI scans during the period,
the manual inspection is performed for three RHI scans in the same volume scan
for every fifteen minutes of data.
The variability of manual estimates increases in time due to growing
undulations at the top of the CBL.
The automatic estimates are consistent and show a smooth CBL growth in time.
The dip in the automatic results at 9:50 CDT is due
to a missing data block in the volume scan;
the transmitter laser beam was turned off when an aircraft
flew into the field of view.
Although the manual estimates have more statistical variations than the
automatic estimates,
they are generally more stable than point measurements of the CBL mean depth.
Since the radiosonde is a point measurement system,
the potential temperature soundings depend on
the distribution of the thermal plumes.
Figure 7 shows plume tops from 600 m to 860 m
and penetration of clear air from 40 m to 340 m when the CBL mean depth
was about 480 m.
Although the radiosonde-based boundary layer depth measurements
closely match with the VIL measurements in this case,
a radiosonde profile may sometimes be measured
through a rising plume or through a downward stream of
free air penetrating deep in the CBL leading to substantial uncertainties.
Furthermore, hourly radiosonde measurements do not provide
detailed information about the growth of the boundary layer.
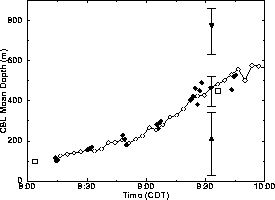
Figure 7: Comparison between manually (solid circles)
and automatically determined (open circles) boundary layer mean depths
on July 28, 1989.
Open squares mark CBL mean depth estimates determined from
potential temperature profiles at 8:01 and 9:36 CDT.
All RHI scans from 9:33 to 9:36 CDT are carefully reanalyzed.
The solid circle at 9:33 CDT shows the average
of the CBL mean depths visually inspected from the RHI scans;
the triangle shows the average altitude of the deepest
downward streams of clear air;
the diamond shows the average altitude of highest
plume tops.
The vertical bars show the minima and maxima of these estimates
from 9:33 to 9:36 CDT.
Potential temperature and specific humidity profiles used in estimating the
CBL mean depths are shown in Figure 8.
Normally, the CBL top is indicated by a sudden potential temperature increase
or specific humidity drop with height.
The potential temperature profile at 8:01 CDT
shows a 100-150 m CBL mean depth, which
is consistent with the VIL measurements.
The CBL depth is difficult to determine from the noisy
potential temperature profile at 9:36 CDT, but
the humidity profile shows a sudden drop
at 400 m indicating that the local
boundary layer top is about 480 m.
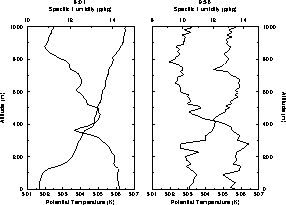
Figure 8: Potential temperature (bold line)
and specific humidity (thin line) profiles measured with
radiosondes on July 28, 1989, at 8:01 and 9:36 CDT.
The VIL elevation from mean sea level
is used as the origin for the altitude axis.



Next: Convective Boundary Layer
Up: Methods for Determining
Previous: Methods for Determining
Return to the Publications.
Return to the Index.
Antti Piironen
Tue Mar 26 20:53:05 CST 1996
 wind speed and a 1 km horizontal
scale of thermals, a vertically pointing lidar
samples across one thermal plume about every six minutes.
An integration over several plume passes is usually
required for obtaining statistically meaningful CBL depth estimates.
When measuring a rapidly growing CBL with a vertically pointing lidar,
averaging times cannot be extended
long enough to dampen the statistical fluctuations without
losing information about sudden changes in the CBL depth.
wind speed and a 1 km horizontal
scale of thermals, a vertically pointing lidar
samples across one thermal plume about every six minutes.
An integration over several plume passes is usually
required for obtaining statistically meaningful CBL depth estimates.
When measuring a rapidly growing CBL with a vertically pointing lidar,
averaging times cannot be extended
long enough to dampen the statistical fluctuations without
losing information about sudden changes in the CBL depth.



 volume
in three minutes, covering typically 10--50 thermal plumes.
Thus, the VIL volume scan
provides similar statistical properties in three minutes
as a vertically pointing lidar does after several hours of averaging.
Furthermore, the scan coverage does not significantly depend on the wind.
Although the CBL depth can be determined
from individual backscatter profiles of the VIL,
the angular scanning enables conversion of the data into more
informative RHI scans.
Then, the CBL structure can be observed by a visual inspection of
the RHI scans providing line averaged measurements
[
volume
in three minutes, covering typically 10--50 thermal plumes.
Thus, the VIL volume scan
provides similar statistical properties in three minutes
as a vertically pointing lidar does after several hours of averaging.
Furthermore, the scan coverage does not significantly depend on the wind.
Although the CBL depth can be determined
from individual backscatter profiles of the VIL,
the angular scanning enables conversion of the data into more
informative RHI scans.
Then, the CBL structure can be observed by a visual inspection of
the RHI scans providing line averaged measurements
[ high
vertical cross section of the CBL.
When a vertically pointing lidar is used to obtain similar spatial
coverage, a one-hour observation time is required in
5 ms
high
vertical cross section of the CBL.
When a vertically pointing lidar is used to obtain similar spatial
coverage, a one-hour observation time is required in
5 ms wind.
wind.
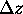 ) and 50 m horizontal spacings,
backscatter signals are mapped on
horizontal Constant Altitude Plan Position Indicator (CAPPI) planes.
Section
) and 50 m horizontal spacings,
backscatter signals are mapped on
horizontal Constant Altitude Plan Position Indicator (CAPPI) planes.
Section  .
Figure
.
Figure 
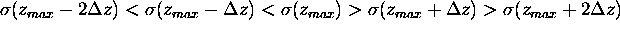 ;
vertical dashed lines highlight the region from
;
vertical dashed lines highlight the region from
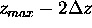 to
to 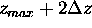 .
Noise-induced variance peaks remain below the average threshold limit.
In this case, peak 2 is selected, since it is the
first peak stronger than the average of the variance profile.
.
Noise-induced variance peaks remain below the average threshold limit.
In this case, peak 2 is selected, since it is the
first peak stronger than the average of the variance profile.  .
It is tested by comparing the mean depths with
manually inspected estimates.
Figure
.
It is tested by comparing the mean depths with
manually inspected estimates.
Figure 

