

The lidar equation of a monostatic lidar system can be presented in the following form

where
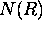 =
number of photons incident on the receiver field of view from
range R per data bin length,
=
number of photons incident on the receiver field of view from
range R per data bin length,
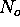 = number of transmitted photons,
= number of transmitted photons,
c = speed of light,
A = area of the receiver telescope,
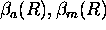 = aerosol and molecular
scattering cross sections per
unit volume, respectively,
= aerosol and molecular
scattering cross sections per
unit volume, respectively,
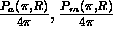 = normalized backscatter
phase function due to aerosol and
molecular scattering, respectively,
= normalized backscatter
phase function due to aerosol and
molecular scattering, respectively,
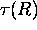 = one way optical depth between lidar and backscatter
volume at
range R,
= one way optical depth between lidar and backscatter
volume at
range R,
= 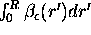 , where
, where
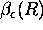 = total extinction
cross section per unit volume,
= total extinction
cross section per unit volume,
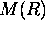 = multiple scattering contribution incident on the receiver
per data bin length,
= multiple scattering contribution incident on the receiver
per data bin length,
B = number of background photons incident on the receiver
per data bin length.
Equation (1) demonstrates that the lidar return depends on both the local value of the backscatter cross section and on the optical depth between the lidar and backscattering volume at range R. A conventional single channel lidar provides a single measurement of N(R) at each range, and therefore it does not provide enough information to solve the lidar equation for extinction or backscatter cross section. The knowledge about the relationship between the backscatter cross section and extinction has to be known or assumed and an estimate of a boundary value has to be given (see for example Klett [23]).
In order to make measurements of extinction and backscatter cross section, the HSRL measures two signals which can be processed to present lidar returns from aerosol and molecule backscattering. The separation between the aerosol and molecular scattering is possible, because the signal backscattered from air molecules is Doppler-broadened, while the signal from more massive, slowly moving aerosols remains spectrally unbroadened.
In the case of the HSRL, two separate lidar equations can be written
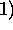 For aerosols
For aerosols
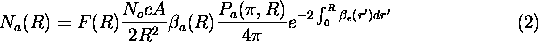
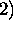 For molecules
For molecules
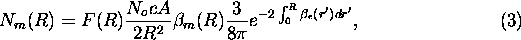
The molecular backscatter phase function is here replaced with
its analytical value  . The term F(R) is an overlap term,
that is a function of receiver and transmitter geometry [8].
Because the molecular scattering cross section
is a function of the air density and can be calculated from
the Rayleigh scattering theory using an independently measured
atmospheric density profile, the equation (3) is well defined and
it can be solved for the extinction.
The molecular scattering cross section
provides a calibration target which is available at each
point of the lidar return.
. The term F(R) is an overlap term,
that is a function of receiver and transmitter geometry [8].
Because the molecular scattering cross section
is a function of the air density and can be calculated from
the Rayleigh scattering theory using an independently measured
atmospheric density profile, the equation (3) is well defined and
it can be solved for the extinction.
The molecular scattering cross section
provides a calibration target which is available at each
point of the lidar return.
Following optical parameters can be obtained from the separated lidar signals:
1) Aerosol to molecular backscatter ratio (scattering ratio) SR(R)
Notice that, the backscatter ratio measurement is not dependent from the overlap term, and therefore measurements of backscatter ratio for the overlap region can be performed. The same effect can be seen later on the aerosol backscatter cross section and depolarization ratio determination.
2) Aerosol backscatter cross section
The properties of the molecular scattering are well known and
therefore, the atmospheric density can be used
to compute the molecular scattering cross section per unit volume 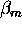 .
From Rayleigh scattering theory [24], the molecular scattering
cross section per unit volume is
.
From Rayleigh scattering theory [24], the molecular scattering
cross section per unit volume is
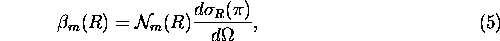
where
 = number of gas molecules per unit volume and
= number of gas molecules per unit volume and
 = differential Rayleigh scattering
cross section at scattering angle
= differential Rayleigh scattering
cross section at scattering angle 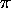 per average gas molecule.
per average gas molecule.
For mixture of atmospheric gases below 100 km altitude [24],

The number of gas molecules per unit volume can be calculated from the atmospheric pressure P(R) and temperature T(R).
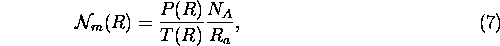
where
P(R) = atmospheric pressure at range R
T(R) = atmospheric temperature at range R
 = Avogadro's number
= Avogadro's number
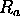 = gas constant of dry air
= gas constant of dry air
Thus, by using the previous equations, the molecular scattering cross section per unit volume can be written in the following form.

where
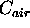 = 3.786 x 10^-6 KhPa^-1m^-1
at 532 nm (from Eq. 5)
= 3.786 x 10^-6 KhPa^-1m^-1
at 532 nm (from Eq. 5)
 = atmospheric pressure
= atmospheric pressure
 = atmospheric temperature
= atmospheric temperature
The aerosol backscatter cross section can be calculated by using the
backscatter ratio and the calculated value of 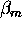
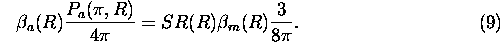
3) The optical depth of a layer between ranges 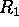 and
and 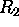
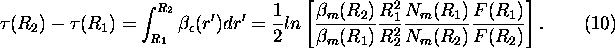
4) Total extinction cross section
The average value of total extinction cross section is a range derivative of the optical depth
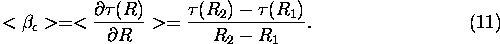
5) Backscatter phase function
The backscatter phase function, 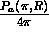 ,
can be calculated from the following
equation
,
can be calculated from the following
equation
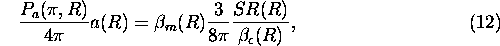
where
 = single scattering albedo.
= single scattering albedo.
For water and ice clouds and most aerosols, the single scattering albedo at the wavelength of 532 nm can be assumed to be unity and therefore the backscatter phase function can be measured.
6) Linear depolarization ratio
The discrimination between water and ice clouds can be made from the depolarization properties of the backscatter signal. The linear depolarization ratio can be given as follows.
where  and
and 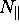 are the number of incident on the receiver
perpendicular and parallel to the receiver polarization axis, respectively.
In the case of the HSRL, separate depolarizations of aerosol
and molecular backscattering can be measured.
are the number of incident on the receiver
perpendicular and parallel to the receiver polarization axis, respectively.
In the case of the HSRL, separate depolarizations of aerosol
and molecular backscattering can be measured.
7) Cloud particle size
By measuring the signal strength variations as a function of field of view, the size of the cloud particles can be measured. The multiple scattered lidar return is a function of receiver field of view, particle size, range from lidar and the optical depth of the cloud. In the HSRL, the multiple scattering information along with the simultaneous single scattering measurement are used to calculate the cloud particle size.A detailed description of the multiple scattering approximation used for the HSRL measurements is presented by Eloranta [25,26] and Eloranta and Shipley [27].